Did you know that there are different sizes of infinity?
I learnt this fact when I was like 11 years old, and it blew my little mind. Let me explain.Imagine the set of natural numbers (1, 2, 3, 4, 5...). How big is that infinity? How about the set of even numbers (2, 4, 6, 8, 10...)? That one's smaller right? You'd think it's half the size, after all, we're taking every other number. That would make sense. But infinity doesn't always make sense.
Let's look at it from a different perspective. What if we assigned a natural number to each even number? Then, we could see how many are left over in the end, and we'd know how much bigger the first set is.
The first even number is two, so we'd pair it with the first natural number, one. Four would get paired with two, six with three, eight with four, and so on.
1, 2, 3, 4, 5, 6, 7, 8, 9, 10...
2, 4, 6, 8, 10, 12, 14, 16, 18, 20...
You might now realise that each natural number has a corresponding even number. There won't be any left over. These two sets are the same size.
How about the rational numbers (the set of fractions)?
The set of rational numbers is also the same size as these first two sets. You can see this if you organize the fractions in a grid, like so: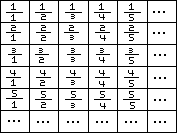
We can draw a line that touches each one of these numbers like this:
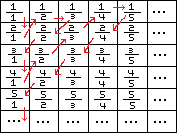
If we were to straighten this line out, we could pair each one of these numbers with the naturals. Even after removing the repeats/equivalent fractions, they are still the same size.
1, 2, 3, 4, 5, 6, 7...
1/1, 2/1, 1/2, 1/3, 3/1, 4/1, 3/2...
What these three sets have in common is that they are all COUNTABLE INFINITIES.
What about the real numbers?
In contrast, the real numbers are an UNCOUNTABLE INFINITY. There is no way to pair them up with the natural numbers. Even the set of numbers between one and zero is bigger than the set of natural numbers. The explanation for this one is a little confusing, but I'll do my best:Suppose you have an infinitely long list of real numbers, each one with infinitely many decimal places. You can create a new number by taking the first digit from the first number, the second digit from the second number, and so on. This will create a unique new number. We know it is not already part of the list as the new number has at least one digit which is different from every number in the set. Infinitely many new numbers can be made this way, which shows that this set is bigger than the set of natural numbers. This proof is called Cantor's Diagonalization argument.